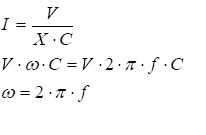POTENCIA DE CORRIENTE CONTINUA: MONTAJE DEL EXPERIMENTO.

 

POTENCIA DE CORRIENTE CONTINUA: MATERIALES Y EQUIPOS y CIRCUITOS DE ANÁLISIS.

MATERIALES Y EQUIPOS.

- Tres resistencias (Focos de 220 V, 200 W).

- Cables de conexión con terminales tipo banana y tenazas con derivación. 

- Multímetro Digital.

- Vatímetro Analógico de laboratorio de precisión.

BV = 600 V BV = 15 – 450 V

BA = 10 A BA = 5 – 10 A 

- Fuente de corriente alterna 220V nominal

CIRCUITOS DE ANÁLISIS.

Conexión Serie:

Conexión Paralelo:

POTENCIA DE CORRIENTE CONTINUA: OBJETIVOS ESPECÍFICOS. y PUNTUACIONES TEÓRICAS.

OBJETIVOS.

- Medición de la Potencia de corriente continúa.

- Interpretación de la Potencia.

- Uso del Ratímetro.

- Interpretación de la papeleta de consumo de la energía eléctrica.

- Interpretación de la placa de un medidor

OBJETIVOS ESPECÍFICOS.

- Ley de Joule.

- Ley de Ohm.

- Unidad de Vatio.

- Transformación de energía.

- Renumeración

- Medición de energía

 PUNTUACIONES TEÓRICAS.

La potencia es la rapidez con la que se realiza un trabajo, es decir, en un determinado tiempo.

El trabajo realizado por una carga eléctrica al desplazarse en un círculo desde un punto A hasta un punto B, es:

W = q (VA - VB)

Si en un circuito existe un receptor que transforma la energía potencial en otra forma de energía, el valor de esta última para un paso de corriente por el receptor durante un tiempo t es:  

W = E = I * t (VA - VB)

Donde: I = q / t

Esta expresión corresponde a la energía consumida por el receptor en WR. La potencia eléctrica en Corriente Continua es aquella que en su totalidad se transforma en otro tipo de energía, cuyo trabajo es útil.

En el interior de un resistor, los electrones se mueven con una velocidad de arrastre constante, sin ganar energía cinética, cuando dicho resistor se somete a una diferencia de potencial eléctrico. La energía potencial eléctrica adquirida por los electrones se pierde y se transmite al resistor en forma de calor. A este efecto, se le llama calentamiento por efecto Joule. Se desarrolla una cierta cantidad de calor que es proporcional a la potencia, esta sigue la siguiente expresión:

P = I2 * R = V2 / R   (W)

Estas ecuaciones se conocen como la Ley de Joule y se aplican solamente en la transformación de energía eléctrica en energía calorífica. Otra forma de expresar la potencia es la siguiente:

P = I * V  (W)

La potencia de renumeración o costo de la energía eléctrica en función del tiempo por [Kwh.]

P =  W * t  [wh] = [Kwh]

 La cantidad de calor que produce un conductor al paso de corriente eléctrica, se encuentra en razón directa a la resistencia, al cuadrado e la intensidad de corriente y al tiempo, su expresión es:

Q = R * I2 * t * 0.24  (Cal)

La potencia en corriente continua se diferencia de la potencia eléctrica en corriente alterna, porque es netamente útil, esto quiere decir que cumple la misión de transformarse en otro tipo de energía aprovechable, sin embargo, este grado de utilidad esta limitado por el rendimiento del equipo a utilizar.

Parámetros R - L - C en Corriente Continua Y Corriente Alterna - CONCLUSIONES

 Finalizada la práctica podemos llegar a las siguientes puntualizaciones más sobresalientes sobre la misma:

De la Resistencia:

• Un elemento resistivo demanda la misma corriente en Corriente Continua y Corriente Alterna a la     misma tensión, porque un amperio en Corriente Alterna calienta una resistencia a la misma                    temperatura que un amperio en Corriente Continua.
• La potencia transformada en una resistencia en Corriente Continua es la misma a la transformada en Corriente Alterna, esta es la misma tensión de alimentación.
• La corriente en Corriente Alterna se mide en valor eficaz y en Corriente Continua en valor medio.
• En Corriente Alterna la potencia en una resistencia está dada por:

   Corriente Continua esta dada por: Vcc Icc

• La forma de onda en ambas fuentes tiene la forma tradicional en Corriente Continua es    unidimensional y en Corriente Alterna es tradicional.

De la Bobina:

• En Corriente Continua una bobina se comporta como cualquier conductor que está en función de su resistencia, vale decir a mayor resistencia menor corriente y viceversa.
• En Corriente Continua se debe tener cuidado del nivel de tensión a aplicar a la bobina, por la      excesiva corriente generalmente debe ser de unos cuantos voltios.
• En Corriente Alterna una bobina se comporta como su nombre lo indica, es decir , cuando circula   corriente por ella crea un gran campo magnético que comparado con la parte resistiva del conductor, es mucho mayor, vale decir, su resistencia a la Corriente Alterna se denomina impedancia.

Por esta razón la corriente demandada por esta es pequeña.

• El factor de potencia en una bobina es 0 idealmente y aproximadamente 90 en una bobina real.
• La forma de onda de la corriente demandada por una bobina es no senoidal por la dependencia del Campo Magnético.
• Los componentes armónicos en la forma de onda son el del 3er  armónico, 5te armónico y 7º armónico.

Del Condensador:

• En Corriente Continua el condensador demanda una pequeña corriente eficiente para el cargado, de unos cuantos Amp.
• El cargado de un condensador se puede medir con un voltímetro de Corriente Continua y Corriente Alterna.
• La tensión define el cargado del condensador, es decir, a menor tensión, menor carga y a mayor tensión, también mayor carga.
• En Corriente Alterna, la corriente demandada por el condensador aumenta en comparación a los Amp. en Corriente Continua.
• Este incremento se debe a la potencia del condensador que es inversamente proporcional a su capacitancia.
• La forma de onda del condensador, es muy difícil de dibujar por el ondulado excesivo.
• Los componentes armónicos en esta carga son del orden 11 y 13 armónicos.
• En general las tres componentes tienen mucha aplicación en Corriente Alterna, la operación de los sistemas se puede llegar a comprender, siempre y cuando se conozcan básicamente a los tres receptores, es decir, desde Corriente Continua y luego en Corriente Alterna.
• La parte resistiva en una resistencia, es sinónimo de trabajo útil.
• La parte inductiva en un sistema es sinónimo de deformación de la forma de onda cuando B / H es no lineal y es sinónimo de bajo factor de potencia.
• La parte capacitiva en un sistema es sinónimo de corriente aletargada a la tensión y también de mucha ondulación en la forma de onda.

BIBLIOGRAFÍA

Circuitos Eléctricos I                              Ing. Oscar W. Anave León.

Circuitos Eléctricos I    Ing. Gustavo A. Nava Bustillo.

Electrotecnia                  GTZ Alemana.

Parámetros R - L - C en Corriente Continua Y Corriente Alterna - CUESTIONARIO Parte 11

Explique la razón por la cual, la forma de onda real de la bobina y el condensador no tienen el lugar geométrico de una función seno o coseno.

La forma de onda de una bobina conectada en Corriente Alterna, no tiene la forma de onda senoidal tal cual vimos en el osciloscopio, la razón de la existencia de esta forma de onda se debe básicamente al siguiente hecho:

• La relación  es diferente a la unidad, razón por la cual existirá un comportamiento alineal de esta relación, ello porque, es el circuito magnético quien se encarga de distorsionar la onda de corriente, por que la corriente demandada por esta tiene una componente fuertemente inductiva, encargada de la inducción del circuito magnético.
• Si la relación B / H tiende a la unidad, entonces estaremos entrando a una zona de comportamiento como filtro de la bobina, es decir, cuando la operación de la bobina no depende exclusivamente del circuito magnético, cuyo comportamiento ahora es lineal.
• Existen tres zonas de comportamiento de la bobina, visto en la práctica, la primera, zona de subsaturación del circuito magnético, donde la forma de onda es no senoidal y la corriente demandada por la bobina es predominantemente reactiva magnetizarte; la segunda, zona de saturación, donde la forma de onda es senoidal y la corriente demandada por la bobina, no es predominantemente reactiva magnetizarte; por último la tercera, zona de sobresaturación, donde la forma de onda es no senoidal, consecuencia del consumo de corriente que es predominante reactiva sobre magnetizarte.

Un condensador distorsiona la forma de onda de corriente, por las constantes de carga y descarga del condensador en función a la frecuencia industrial de la alimentación.

La forma de onda del condensador varía en función de los siguientes parámetros:

• Frecuencia, si esta es menor, la forma de onda se mejorará.
• Corriente de fuga, si esta es mayor, la forma de onda se mejora apreciablemente.

Parámetros R - L - C en Corriente Continua Y Corriente Alterna - CUESTIONARIO Parte 10

 

Podemos observar que se a opuesto al paso de la corriente al conectar un resistor adicional (la bombilla se enciende con retraso), esta resistencia es grande al principio (la bombilla estaba apagada) y pequeña después del proceso de conmutación (gran luminosidad). Cuando varía la intensidad de la corriente en la bobina, aparecerá simultáneamente un campo magnético variable, que provoca un fenómeno de inducción (Ley de Faraday). La nueva tensión inducida se opone a la tensión exterior, la conectada al circuito (Ley de Lenz), con lo que esta última sólo podrá aumentar paulatinamente. La tensión inducida desparece cuando la intensidad de la corriente ya no varía.

En una bobina aparece una tensión de autoinducción cuando varía la intensidad de la corriente.

El resultado del experimento y los razonamientos consiguientes nos han mostrado que la corriente y la tensión en una bobina varían en sentidos opuestos. La corriente parte de una intensidad nula al conectar y crece poco a poco hasta alcanzar su valor máximo. La tensión total se reparte entre la bobina y la bombilla (conexión serie). En el instante de cierre, la tensión en la bobina ha de ser máxima. Al aumentar la intensidad irá decreciendo la tensión en la bobina y aumentando en la bombilla (que se enciende).

Parámetros R - L - C en Corriente Continua Y Corriente Alterna - CUESTIONARIO Parte 9

 9. Explique las  diferencias que existe en la operación de los parámetros RLC en Corriente Continua y en Corriente Alterna.

- Como podemos ver en el parámetro R, la tensión esta en base a la corriente, lo cual se puede ver en         

    el diagrama senoidal (𝟇 = 0º).

- Para el parámetro L vemos que la tensión está adelantada en T/4 (un cuarto de periodo con relación    

    a la corriente) o sea (𝟇 = 90º).

- Finalmente en el parámetro C la tensión está T/4 atrasada (un cuarto del periodo atrás con la    

    corriente), o sea (𝟇 = - 90º).

- La corriente que demanda en Corriente Continua está limitada por la resistencia de la bobina, pero como generalmente esta es pequeña, entonces la corriente es muy grande y en Corriente Alterna la corriente está limitada no sólo por su resistencia, sino también por la reactancia que es función del número de espiras y de la sección del núcleo.

- La corriente que demanda este parámetro en Corriente Continua es muy pequeña, suficiente para el cargado de las placas de acuerdo a la tensión aplicada y el tiempo de cargado es muy pequeño. En Corriente Alterna la corriente es constante, es decir, nos indica el cargado y descargado del condensador, pero en función directa de la frecuencia y capacidad, es decir: